| 閉じる | ||
| 【発明の名称】回帰分析の”多重共線性”等を解消し、説明変数の適切な目的変数への寄与度を示す偏回帰係数を求めて経営資料とする計算技術。 【出願人】 【識別番号】506259944 【氏名又は名称】白井 雅浩 【住所又は居所】東京都江戸川区東葛西9丁目10番1 313号 【発明者】 【氏名】白井 雅浩 【住所又は居所】東京都江戸川区東葛西9丁目10番1 313号 【要約】 【課題】 産業の成果Yと原因Xiとの関係分析に適用される重回帰分析は、選択される原因の説明変数に目的変数Yとの相関の相当程度高い数値のものが多い。これが成果Yに対する寄与度を示す原因の説明変数Xiの偏回帰係数biを理論、経験から離れたものにさせる。 【解決手段】 この矛盾を解消するために、重回帰分析の正規方程式の成果Y、説明変数Xiの相関係数の行列式を作成し、左右両辺の数値バランスが取れていないことから行列の主力変数である対角要素Xiを基準に従属的非対角要素のXjからXiとの重複分を除去して剰余分を、これを改めて行列の非対角要素とした正規方程式の新相関行列式のbiを求めることにより、”多重共線性”等を解消する計算技術である。 【特許請求の範囲】 【請求項1】 売上高等を目的変数Yとし、販売経費等を説明変数Xiとする重回帰分析の正規方程式、Y,Xiを基準化変数(A=(Xi−Xi)/σi,Xi:平均、σi:標準偏差、Yも同様)とする正規方程式の相関行列式を作成し、の基準化変数を数値の統一と重複分除去で負数を生じないよう一定数を加算した行列の対角要素を基準変数、非対角要素を従属変数として、従属変数から基準変数との重複分を除去し、残余を改めて正規方程式の相関行列式の非対角要素とした新行列式からYへの寄与度を示す偏回帰係数biを求める”多重共線性“等を解消する計算技術である。 【発明の詳細な説明】 【技術分野】 【0001】 本発明は、産業上の成果である売上高等と原因である販売経費等の関係を重回帰分析で行う際に生ずる“多重共線性”等の問題を解消し、売上高に寄与する販売経費などの原因変数の寄与度を示す適切な偏回帰係数biを求めることを目的とする計算技術である。 【背景技術】 【0002】 重回帰分析を適用し、成果と原因の関係を解明する場合に、説明変数に“多重共線性”等の問題が生じ、適切な経営判断ができない。このことを次の仮設分析例で”多重共線性”による偏回帰係数biの歪みを、また、説明変数間にある程度高い相関のある場合のbiの歪みを示す。 【0003】 重回帰式 Y=b0+b1X1+b2X2 (1) 基準化した変数の重回帰式 Ay=bA1+b2A2 (2) 仮設分析例 売上高とその原因である人件費、売場面積は次のようであるとする。 売上高(百万円) 人件費(10万円) 売場面積(10m2) Y X1 X2 A店 46 97 75 B店 18 61 59 C店 36 83 72 D店 22 37 51 E店 27 75 48 この資料に対して説明変数が2ケである場合の重回帰分析を適用する。 この計算結果は、次の通りである。 売上高対人件費の相関係数 R1 :0.84 売上高対売場面積の相関係数 R2 :0.79 人件費対売場面積の相関係数 r12 :0.72 b1=0.56 b2=0.38 売上高に対する人件費、売場面積の相関係数にそれほど差がないのに、原因の成果に対 する寄与度を示す偏回帰係数b1、b2の数値に大きな差がある。これは人件費、売場 面積の間に相当程度の高い相関があることによるものであり、実務経験者である経営者 もこの分析結果の妥当性に疑問を持つ。 【0004】 分析例2(実施例3より、分析結果だけを示す。) 事例名 J K L 目的変数に対する 相関係数:R 0.51 0.62 0.54 偏回帰係数: bi 0.10 0.43 0.33 これは適当に作られた事例についての分析だが、事例Jの相関係数に対する偏回帰係数 の数値が小さい。これは実施例の説明変数相互の相関係数の数値が0.5前後とやや大 きいことによるが、この程度の数値なら特別高い相関とは言えない。 【0005】 回帰分析は一組(X1,X2,..,Xp)の説明変数が目的変数Yをどれだけ説明できるかの分析で、原因となるXiの数値は物理学、化学等による独立性の高いものであったとされ、一組を構成する構成要素個々のXiの貢献度を求めるものではなかったとされる。その後、社会経済現象の成果である企業の売上高とその原因である販売諸経費の関係分析に、重回帰分析が利用されるようになると、採用する諸原因は売上高と高い因果関係のある人件費、販売経費、売場面積等が選択されるようになり、売上高数値を媒介としてそ れら原因間の相関係数も高く、売上高への寄与度を示すbiも常識、理論に反する異常値を示すようになった。これが”多重共線性“の問題である。 【0006】 基準化変数 上記の(1)式について、説明変数Xiの数値単位が人数であったり面積m2であったりすると、求められるbiの数値の意味が曖昧となるので、以後の分析で多用される相関行列の作成に変数を基準化する必要があることから、変数は全て基準化数値を使用する。 以下A1,A2はX1、X2の基準化した変数である。 基準化 :Ai=(Xi−Xi)/σi (3) の平均 σi:Xiの標準偏差 なお、Y,X1,X2を基準化することにより、Aiの数値は平均0、標準偏差1の数値集団となる。 【0007】 正規方程式の相関行列 以下の分析では主に重回帰分析の正規方程式の相関行列式を多用するので、ここでこれを導入する。 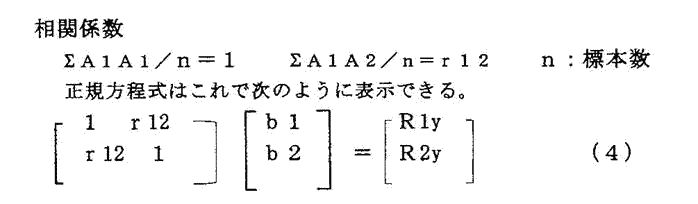 【0008】 特許文献1 特許第5120820号「”多重共線性“を解消する回帰分析によって適正な標準宅地の評価を行う装置」 ”多重共線性”の解決は、正規方程式の行列表示で、左右両辺の項目数値のアンバランスをいかに合理的に抑えるかにかかっている。この特許は説明変数が2変数の場合で、目的変数である地価の媒介による説明変数相互の比較的高い相関部分を次のように除去して、行列第1行の非対角要素2項を構成している。 r12=r12(1−R1R2) これは個々の事例についてではなく、一連の事例に対してR1R2の数値を一括除去する方法である。この除去により、それなりに”多重共線性“を解消する効果を期待できるが大まかな計算である。 特許文献2 特許第5585921号「産業上の成果である売上高等と原因である販売経費等の関係分析に”多重共線性“解消の重回帰分析を適用して解明する装置」 この特許の”多重共線性“解消は[特許文献1]の除去に比して、個別の事例を対象としたより丁寧な除去であるが、基準化した説明変数そのものに対する除去であるため、事例を基準化変数の正と負の符号同調事例に分類し、それぞれについて行うもので、一貫性がなく、求めた相関行列も非対称行列になっている。 【0009】 ”多重共線性“問題を回避するために一般に次のような方法が考えられている。 相関の高い説明変数のどちらか一つの削除 主成分分析 リッジ回帰 説明変数の削除は成果である売上高に対して有意に選択された原因である従業員数や販売経費を省くのは適切でない。 主成分分析はP個の変数X1,X2,..Xpをある条件の下にp>mの綜合変数j(j=1〜m)に要約する方法で、説明変数の係数biを求めるものではない。 リッジ回帰は相関行列の対角要素に一定数kを加えて偏回帰係数を求めるもので、概要を次に示す。 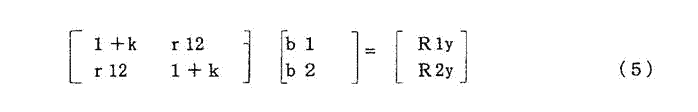 これは、非対角要素の相関係数r12の数値を小さくする効果があり、その分だけ“多重共線性”が解消されるが、相関行列の対角要素に加える加算数値の選択に確たる基準がなく、恣意的であまり利用されていないと思う。 【非特許文献1】Arthur E.Hoer and Robert,W.Kennard“Ridge regression”1970年 2月 【発明の開示】 【発明が解決しようとする課題】 【0010】 リッジ回帰の”多重共線性“解消は対角要素を対象として非対角要素数値を小さくする間接的方法であるのに対して、本発明は相関行列の非対角要素を直接の分析対象とする。 【0011】 数式(4)の第1行をみれば、左辺は原因変数X1とX2との相関係数の和で、(1+r12)は、変数選択の経緯からr12は0より大きい正数と考えられるから1より大きい数値となり、右辺のR1(1>R1>0)より数値が大となる。だから、左辺、右辺の等号を満足させるには次のような方法が考えられる。 第1の方法は現行の回帰分析の手法で、いわば強引に左右両辺の等号を図る方法と言える。 多重共線性“問題を発生させる。 第2の方法は、数式(4)が原因変数2ケ以上で、左辺各項の原因変数値に重複が予想される場合に、その重複分を除去するものである。この場合でもなお左右両辺の数値は残るが大幅に緩和される。この操作の適否は、除去方法が理論的、実務的に合理的であるか否かによる。左辺第1行の最初の項はX1の相乗であり、右辺はまた目的変数YとX1だけの相関なので、この行に関してX2は従属的立場の変数である。だから、変数間の重複分を除去するとすれば主力的なXiを基準に従属的立場のX2から除去するのが適切と考える。 【課題を解決するための手段】 【0012】 1 基準化変数Aiは、これに一定数を加算、乗算しても元のAiの数値は不変である。 基準化式(3)参照 2 ΣA1A2/n=r12 である。 3 Aiの数値のままでの重複分除去は、負数がある場合は計算が複雑になるので、除去 計算で全て正数になるように、又、全てのAi数値が統一された数値となるように一定 数(本実施例ではAの負数最大値を目途に.1.8)を加算する。 4 左辺(対角要素A1、非対角要素A2)について、A2からA1と同調する部分を下記の通り除去するため、A2とA1の絶対値のどちらか低い数値を限度としてA2から除去し、残余分を求める。 する除去例 A1 A2 除去分 残余分 0.3 0.2 0.2 0 0.2 0.5 0.2 0.3 なお、上記3の一定数加算で実施例のA1,A2の数値総和は18と等しくなる。 このことから、次の簡単な例で理解できるように正規方程式は、正方行列で斜線状に位置 する対角要素の対称の位置にある非対角要素の数値は等しくなる。 A1、A2の数値総和を等しく0.7とする。 A1が対角要素(除去基準)でA2が除去される非対角要素である場合 A1 A2 除去分 残余分 0.3 0.5 0.3 0.2 0.4 0.2 0.2 0 逆の場合 A2 A1 除去分 残余分 0.5 0.3 0.3 0 0.2 0.4 0.2 0.2 このため正規方程式の相関行列の斜線状の対角要素を基準とした対称の位置にある非対 角要素の数値は等しい。 5 除去残余分はA2の一部なので、これをA1*A2(これは重複分除去前の相関係数 r12である。数式(4)参照)に乗じ、改めてr12を求めて重複分除去後の新相関 行列を作り、重複分除去後のbi(i=1,2)を求める。 【発明の効果】 【0013】 求めたbiの妥当性を確認するため、目的変数Yに対する説明変数の元の最高相関係数を100とした場合のbiの相対比を求めると、元の相関数値に近く,“多重共線性”等が解消されていることが分る。 【実施手順】 1 多重回帰分析の正規方程式の目的変数Y,説明変数Xiを、説明変数の計測単位によ る変動を抑制するために、また、正規方程式の相関行列を作成するために各変数の基 準化を行う。 2 基準化変数の一定数加算.乗算により数値が変化しない特性を利用する。 3 正規方程式の各行の数値ために、また、重複分除去により負数を生じさせないように するために基準化変数に一定数の加算をする。 4 対角である主力変数を基準とした非対角要素の従属変数の重複分除去は[0012] の計算を適用する。 5 求められた残余の数値は行列の非対角要素である従属変数の一部なので[0012] 、改めて正規方程式の非対角要素の相関係数とする新行列式を作る。 6 以上の演算よる正規方程式の新行列から、目的変数Yへの寄与度を示すbiを求める 。 7 ここまでの“多重共線性”等解消の演算方法が適切である否かを検証するために、同 一事例に対して説明変数を順次追加させた場合の当該方法の妥当性を検証する。これ を見ると説明変数4ケの場合に適用した“多重共線性”等の解消の演算方法の結果は 、元の目的変数に対する説明変数の相関係数の相対比格差に近く概ね妥当である。 【実施例】 実施例1 以下の目的変数Y,説明変数Xh,Xi,Xj,Xk,Xlは適当に設定した数値です。計算を簡単にするため各変数相互の相関係数を求める。 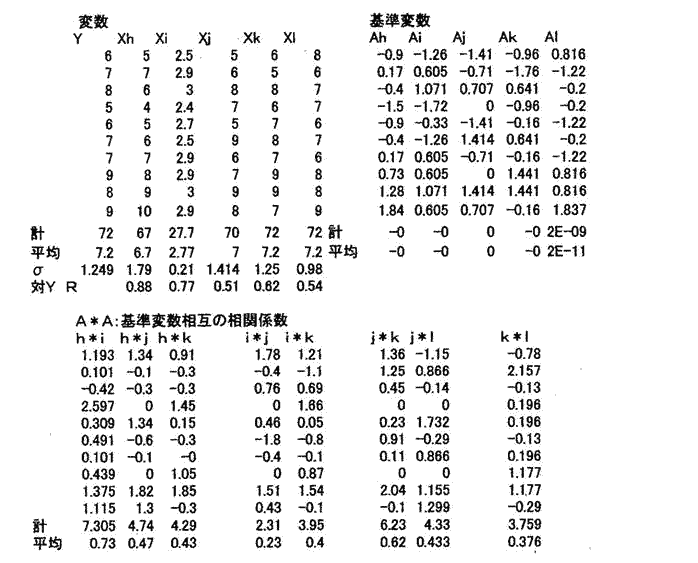 実施例2 2変数、3変数、4変数の場合  計算結果は採用変数2変数、追加しiた3変数、4変数の全ての場合で、現行分析方法で求めたbi数値は乱れているが、重複分除去の分析ではいずれの場合もR値の相対比に比較的近い結果得ている。 実施例3 Yに対する相関係数が0.5レベルの事例xj,Xk,Xlの3事例についてのbiを求める回帰分析である。 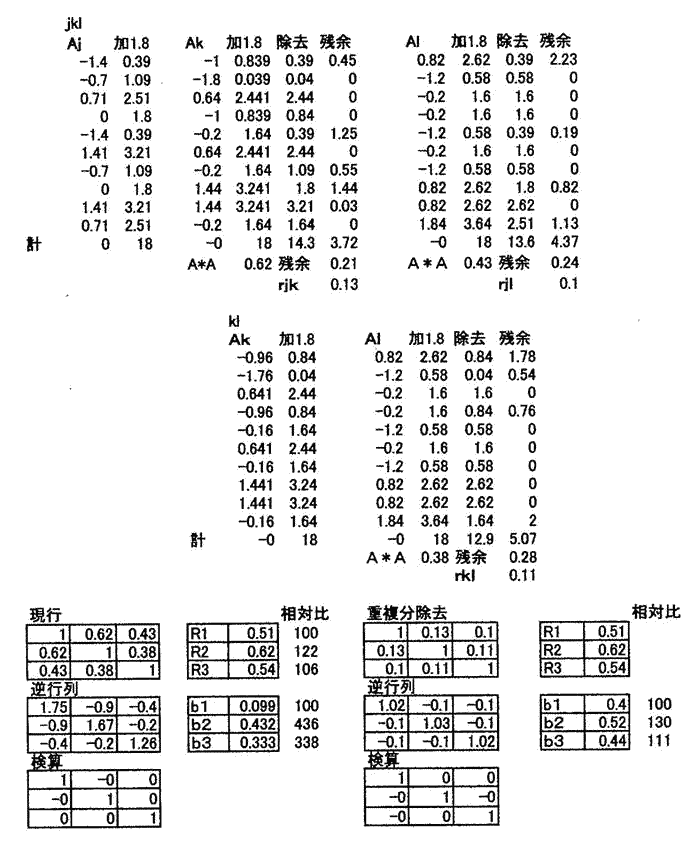 計算結果は現行分析方法のb値は乱れているが、重複分除去の計算でほぼR値に近い。 |
||
| ページtop へ | ||